Algebra 1 (covid19 Work)

 



Purplemath

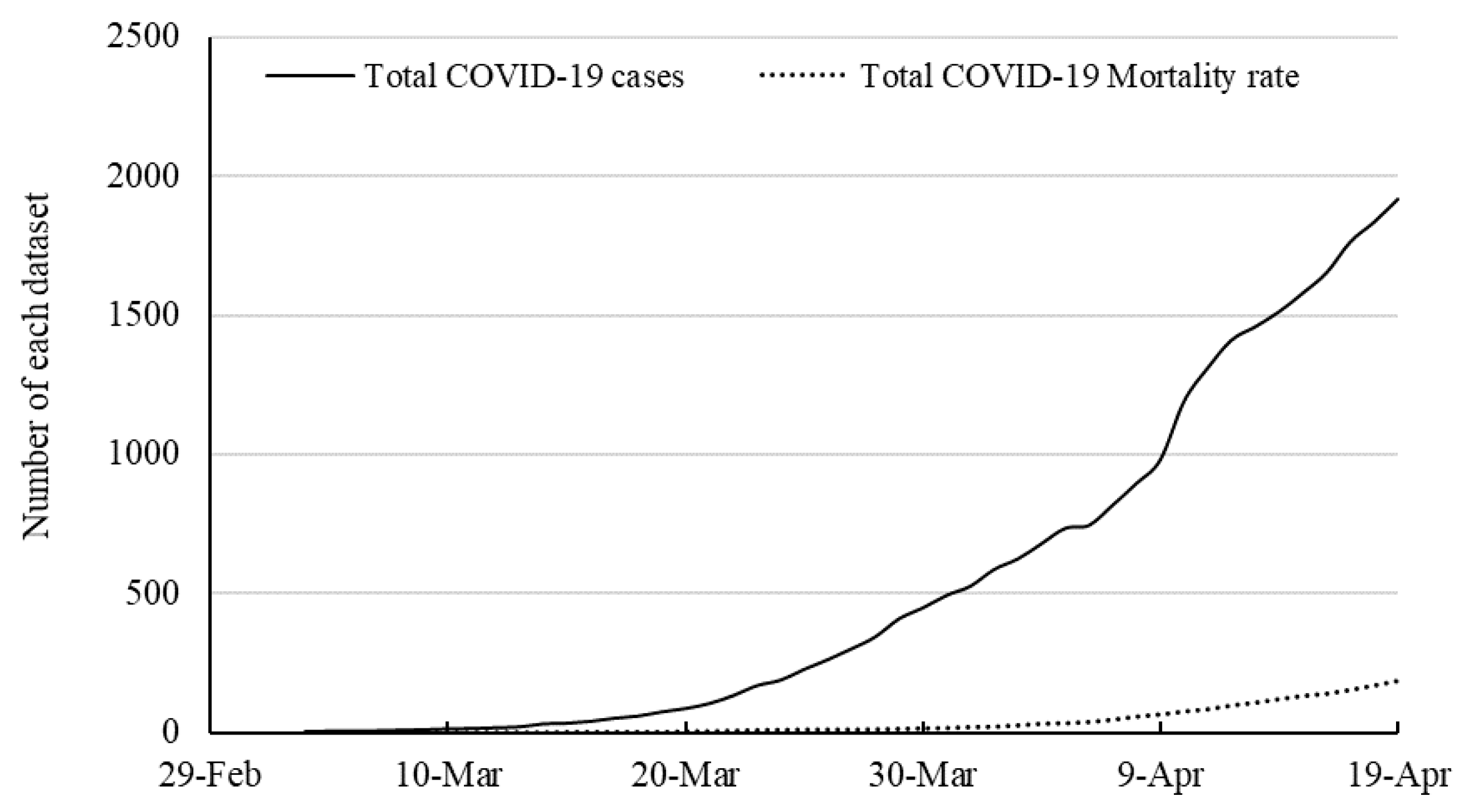
In clinical trials, hypersensitivity-related adverse events were observed in 0.63% of participants who received the Pfizer-BioNTech COVID-19 vaccine and 1.5% of participants who received the Moderna COVID-19 vaccine, compared to 0.51% and 1.1%, respectively, in the placebo groups. Coronavirus Research Archive. In response to the COVID-19 pandemic, Taylor & Francis is making relevant research articles free to access in order to support the global effort to diagnose, treat, prevent COVID-19.

Mathematics—3 years. Must include first-year algebra and two additional years of college-preparatory mathematics, including Algebra II (or equivalent) or higher. An advanced mathematics course is highly recommended in your senior year. One year of either algebra or geometry taken prior to ninth grade are acceptable. Science—3 years. In this lesson students work to see a binomial expression as a single entity and learn how to factor a common binomial expression from a more complex express.

'Work' problems usually involve situations such as two people working together to paint a house. You are usually told how long each person takes to paint a similarly-sized house, and you are asked how long it will take the two of them to paint the house when they work together.

Many of these problems are not terribly realistic — since when can two laser printers work together on printing one report? — but it's the technique that they want you to learn, not the applicability to 'real life'.

The method of solution for 'work' problems is not obvious, so don't feel bad if you're totally lost at the moment. There is a 'trick' to doing work problems: you have to think of the problem in terms of how much each person / machine / whatever does in a given unit of time. For instance:

MathHelp.com

  • Suppose one painter can paint the entire house in twelve hours, and the second painter takes eight hours to paint a similarly-sized house. How long would it take the two painters together to paint the house?

If the first painter can do the entire job in twelve hours and the second painter can do it in eight hours, then (this here is the trick!) the first guy can do 1/12 of the job per hour, and the second guy can do 1/8per hour. The question then becomes, how much then can they do per hour if they work together?

To find out how much they can do together per hour, I make the necessary assumption that their labors are additive (in other words, that they never get in each other's way in any manner), and I add together what they can do individually per hour. So, per hour, their labors are:

Algebra 1 (covid19 Work)Algebra 1 (covid 19 work) 17

1/12 + 1/8 = 5/24

In other words, they can do 5/24 of the job per hour.

But the exercise didn't ask me how much they can do per hour; it asked me how long they'll take to finish one whole job, working togets. So now I'll pick the variable 't' to stand for how long they take (that is, the time they take) to do the job together. Then they can do:

1/t per hour

This gives me an expression for their combined hourly rate. I already had a numerical expression for their combined hourly rate. So, setting these two expressions equal, I get:

5/24 = 1/t

I can solve by flipping the equation; I get:

t = 24/5 = 4.8 hours

An hour has sixty minutes, so 0.8 of an hour has forty-eight minutes. Then:

They can complete the job together in 4 hours and 48 minutes.

Content Continues Below

The important thing to understand about the above example is that the key was in converting how long each person took to complete the task into a rate.

Each person took a certain number of hours to complete the task:

hours to complete job:

Since the unit for completion was 'hours', I converted each time to an hourly rate; that is, I restated everything in terms of how much of the entire task could be completed per hour. To do this, I simply inverted each value for 'hours to complete job':

completed per hour:

first painter: 1/12

second painter: 1/8

together: 1/t

Then, assuming that their per-hour rates were additive, I added the portion that each could do per hour, summed them, and set this equal to the 'together' rate:

adding their labor:

(covid19

1/12 + 1/8 = 1/t

Algebra 1 (covid 19 work) 17

5/24 = 1/t

24/5 = t

As you can see in the above example, 'work' problems commonly create rational equations. But the equations themselves are usually pretty simple to solve.

  • One pipe can fill a pool 1.25 times as fast as a second pipe. When both pipes are opened, they fill the pool in five hours. How long would it take to fill the pool if only the slower pipe is used?

My first step is to list the times taken by each pipe to fill the pool, and how long the two pipes take together. In this case, I know the 'together' time, but not the individual times. One of the pipes' times is expressed in terms of the other pipe's time, so I'll pick a variable to stand for one of these times.

Affiliate

Advertisement

Algebra 1 (covid 19 Work) 64

You might wonder how to work with that '1.25 times as fast' part. If you're not sure, try doing similar computations with simpler numbers. For instance, if the faster pipe filled the pool 2 times as fast as the second pipe, then it would take one-half as long to fill the pool. If the faster pipe filled the pool 3 times as fast as the second pipe, then it would take one-third as long to fill the pool. Following this same reasoning, since the faster pipe fills the pool 1.25 = 5/4 as fast as the second pipe, then it takes 4/5 as long as does the second pipe to fill the pool.

Since the faster pipe's time to completion is defined in terms of the second pipe's time, I'll pick a variable for the slower pipe's time, and then use this to create an expression for the faster pipe's time:

hours to complete job:

slow pipe: s

fast pipe: 4/5s

together: 5

Next, I'll convert all of the completion times to per-hour rates:

completed per hour:

slow pipe: 1/s

fast pipe: 5/(4s)

together: 1/5

Then I make the necessary assumption that the pipes' contributions are additive (which is reasonable, in this case), add the two pipes' contributions, and set this equal to the combined per-hour rate:

adding their labor:

1/s + 5/(4s) = 1/5

multiplying through by 20s (being the lowest common denominator of all the fractional terms):

They asked me for the time of the slower pipe, so I don't need to find the time for the faster pipe. My answer is:

The slower pipe takes 11.25 hours.

Affiliate

Affiliate

Note: I could have picked a variable for the faster pipe, and then defined the time for the slower pipe in terms of this variable. If you're not sure how you'd do this, then think about it in terms of nicer numbers: If someone goes twice as fast as you, then you take twice as long as he does; if he goes three times as fast as you, then you take three times as long as him. In this case, if he goes 1.25 times as fast, then you take 1.25 times as long. So the variables could have been 'f ' for the number of hours the faster pipe takes, and then the number of hours for the slower pipe would have been '1.25f '.

URL: https://www.purplemath.com/modules/workprob.htm

Below are the standard admission requirements for freshmen. See the requirements for:

  • Transfer students
  • International students
A. Graduate from a standard or accredited high school.

Algebra 1 (covid 19 Work) 20

Check to see if your high school is on the list of regional accreditors.
B. Earn a C– or better in 15 college preparatory courses.
  • English—4 years. All four years should be in preparatory composition and literature with emphasis on and frequent practice in writing expository prose.
  • Mathematics—3 years. Must include first-year algebra and two additional years of college-preparatory mathematics, including Algebra II (or equivalent) or higher. An advanced mathematics course is highly recommended in your senior year. One year of either algebra or geometry taken prior to ninth grade are acceptable.
  • Science—3 years. Must include a year each in two fields of college-preparatory science such as biology, chemistry, physics, or earth and physical science. One year of laboratory science is recommended.
  • Social Studies—3 years. Complete three years of social studies from such areas as global studies, history, or social studies electives.
  • Second language—2 years. The UO offers several options for meeting the second-language requirement.
Self-reported transcript information (Self-Reported Academic Record (SRAR) must be provided in order for your application to be reviewed. Prior to enrolling at the UO, submit a final official transcript confirming graduation and showing all academic course work. If you have completed dual-enrollment or college (post-secondary) we would need a copy of your official college or dual-enrollment transcript prior to enrollment.
D. Submit SAT or ACT scores.
Effective with applicants for fall 2021 or beyond, submitting scores from the SAT/ACT is now optional for admissions. Many students will still provide scores, so if you do send them, we prefer scores to be sent directly from the testing service. We also accept scores reported on official high school transcripts. Our school code number for the SAT Reasoning Test is 4846; our code for the ACT is 3498.
Wondering whether to submit your scores? Visit our Test Optional FAQ page.
E. Submit an application essay.
The UO is interested in learning more about you. Write an essay of 650 words or less that shares information that we cannot find elsewhere on your application. Any topic you choose is welcome. Some ideas you might consider include your future ambitions and goals, a special talent, extracurricular activity, or unusual interest that sets you apart from your peers, or a significant experience that influenced your life. If you are applying to the UO's Robert D. Clark Honors College, feel free to resubmit your honors college application essay.
F. Optional second essay.
As you’ve looked into what it will be like to attend Oregon, you’ve hopefully learned about what makes Ducks Ducks. No two are alike, though, so tell us what makes you you, and how that connects to our campus community. We are interested in your thoughts and experiences recognizing difference and supporting equity and inclusion, and choosing one of these two options will guide you in sharing those thoughts. You can learn more about equity and inclusion at Oregon by visiting the Equity and Inclusion website. Maximum statement length is 500 words. This statement is not required.

Algebra 1 (covid 19 Work) 12

Now that you know what the requirements are, read about how we evaluate your application or start your application online.

Algebra 1 (covid 19 Work) 18

Alternative Admission

Algebra 1 (covid 19 Work) 17

If you do not meet one or more of the standard admission requirements, review the options for alternative admission, including information for students from nonaccredited high schools. Also, see the requirements for homeschooled students and students who earned a GED.